

Answer: A
Solution:
Simplifying the given expression, we get: (6?3)=2.

Answer: C
Solution:
It is 2/3 of 90. 90*2/3=60.

Answer: D
Solution:
D is 0.
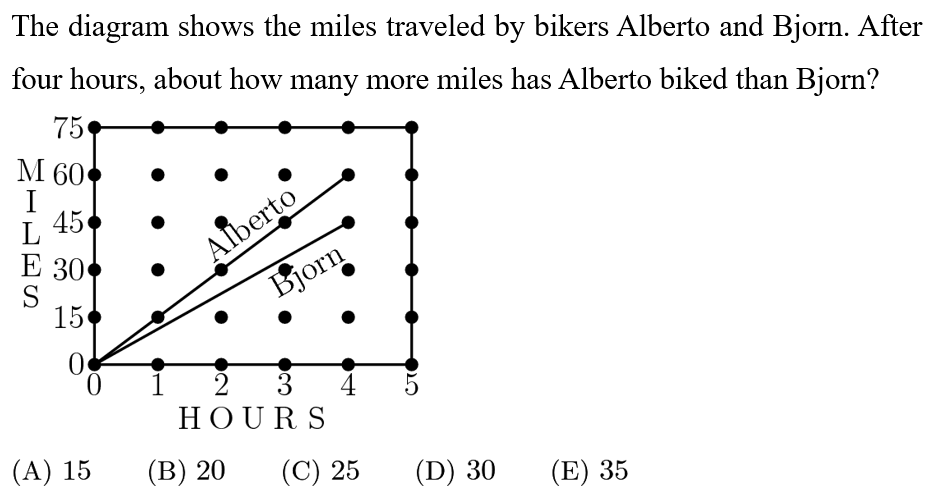
Answer: A
Solution:
After 4 hours, we see that Bjorn biked 45 miles, and Alberto biked 60. Thus the answer is 60-45=15.

Answer: D
Solution:
The perimeter of the rectangular garden is 2*(50+10)=120 feet. A square with this perimeter has side length 120/4=30 feet. The area of the rectangular garden is 50*10=500 and the area of the square garden is 30*30=900, so the area increases by 900-500=400.

Answer: E
Solution:
Use logic to solve this problem. Neither Jo nor Bo has as much money as Flo. So Flo clearly does not have the least amount of money. Rule out Flo. Both Bo and Coe have more than Moe. Rule out Bo and Coe; they clearly do not have the least amount of money. Jo has more than Moe. Rule out Jo. The only person who has not been ruled out is Moe. So E is the answer.

Answer: E
Solution:
There are 160-40=120 miles between the third and tenth exits, so the service center is at milepost 40+(3/4)*120=40+90=130.

Answer: A
Solution:
When G is arranged to be the base, B is the back face and W is the front face. Thus, B is opposite W.
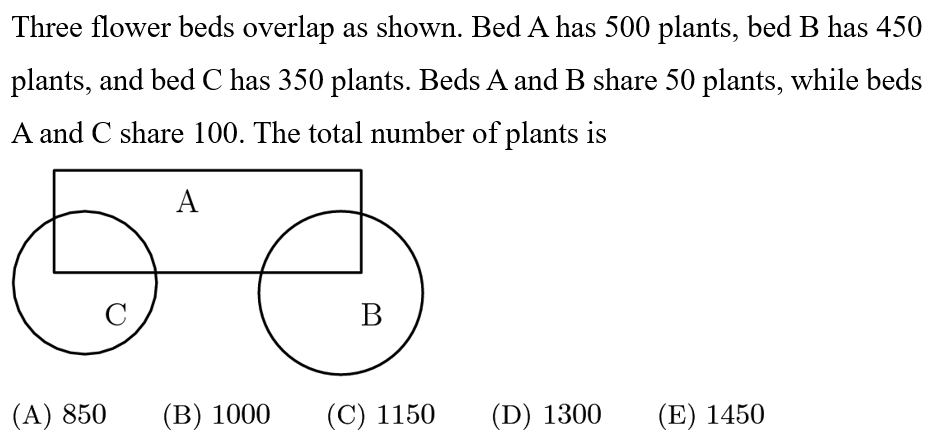
Answer: E
Solution:
Plants shared by two beds have been counted twice, so the total is 500+450+350-50-100=1150.

Answer: E
Solution:
The probability of green is 25/60=5/12, so the probability of not green is 1-5/12=7/12.

Answer: D
Solution:
The largest sum occurs when 13 is placed in the center. This sum is13+10+1=13+7+4=24. Note: Two other common sums, 18 and 21, are also possible.

Answer: B
Solution:
4/(11+4)=27%

Answer: C
Solution:
First, find the total amount of the girl's ages and add it to the total amount of the boy's ages. It equals 20*15+15816=540. The total amount of everyone's ages can be found from the average age, 17*40=680. Then you do680-540=140 to find the sum of the adult's ages. The average age of an adult is divided among the five of them, 140/5=28.
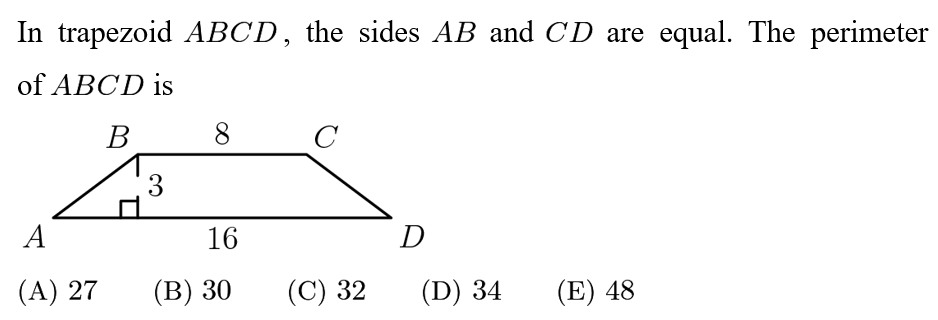
Answer: D
Solution:
There is a rectangle present, with both horizontal bases being 8 units in length. The excess units on the bottom base must then be 16-8=8. The fact that AB and CD are equal in length indicate, by the Pythagorean Theorem, that these excess lengths are equal. There are two with a total length of 8 units, so each is 4 units. The triangle has a hypotenuse of 5, because the triangles are 3-4-5 right triangles. So, the sides of the trapezoid are 8,5,16,and 5. Adding those up gives us the perimeter,8+5+16+5=34.

Answer: D
Solution:
There are currently 5 choices for the first letter, 3 choices for the second letter, and 4 choices for the third letter, for a total of 5*5*4=60 license plates. In general, when three numbers have the same fixed sum, their product will be maximal when they are as close together as possible. This is a 3D analogue of the fact that a rectangle with fixed perimeter maximizes its area when the sides are equal (ie when it becomes a square). In this case, no matter where you add the letters, there will be 5+3+4+2=14 letters in total. If you divide them as evenly as possible among the three groups, you get 5,5,4, which is a possible situation. The answer is 5*5*4-5*3*4=100-60=40

Answer: B
Solution:
First, calculate how many of each type of problem she got right:
Arithmetic: 70%*10=7;
Algebra: 40%*30=12;
Geometry: 60%*35=21;
Altogether, Tori answered7+12+21=40 questions correct. To get a 60% on her test overall, she needed to get 60%*75=45 questions right. Therefore, she needed to answer 45-40=5 more questions to pass.

Answer: C
Solution:
If 108 students eat 2 cookies on average, there will need to be 108*2=216 cookies. There are 15 cookies per pan, meaning there needs to be 216/15=14.4 pans. However, since half-recipes are forbidden, we need to round up and make 15 pans. 1 pan requires 2 eggs, so 15 pans require 2*15=30 eggs. Since there are 6 eggs in a half dozen, we need 30/6=5 half-dozens of eggs, and the answer is C.

Answer: E
Solution:
If there were 108 students before, with the 25% of students missing, there will be 75% of 108 students left. This is 75%*108=81 students. These students eat 81*2=162 cookies. 162/15=10.8 pans. However, since half-recipes are forbidden, we need to round up and make 11 pans.
Answer: B
Solution:
For 216 cookies, you need to make 215/15=14.4 pans. Since fractional pans are forbidden, round up to make 15 pans. There are 3 tablespoons of butter per pan, meaning 3*15=45 tablespoons of butter are required for 15 pans.Each stick of butter has 8 tablespoons, so we need 45/8=5.6 sticks of butter. However, we must round up again because partial sticks of butter are forbidden! Thus, we need 6 sticks of butter, and the answer is B.
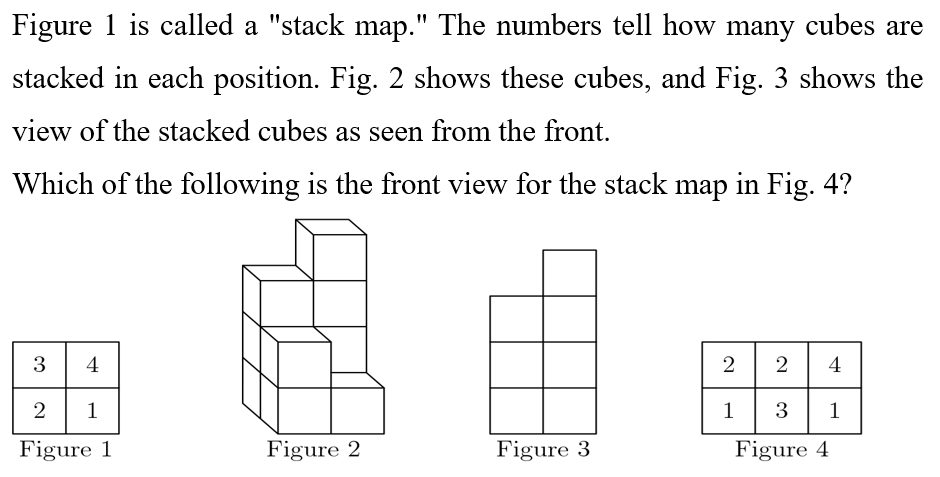
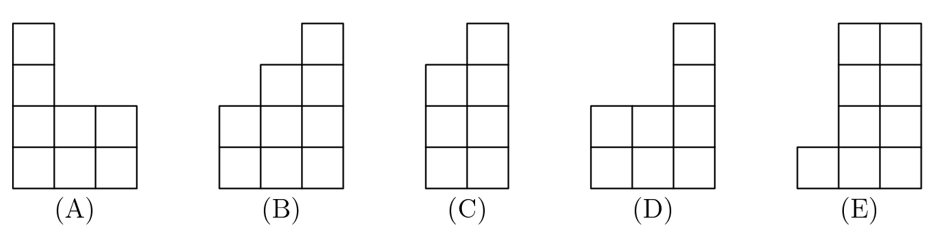
Answer: B
Solution:
The third view is a direct, head-on view of the cubes. Thus, you will only see the highest (or, in these cases, higher) tower in each up-down column. For figure 4:
The highest tower in the first up-down column is 2 in the upper-left box.
The highest tower in the second up-down column is the 3 in the lower-middle box.
The highest tower in the third up-down column is the 4 in the upper-right box.
Thus, the head-on view of this tower should have 2 boxes on the left, 3 in the middle, and 4 on the right. Diagram B shows this description.
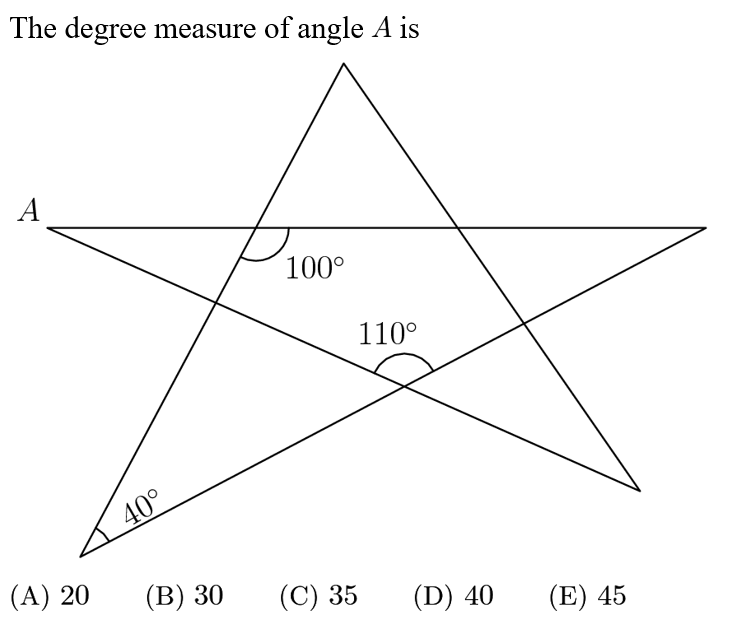
Answer: B
Solution:
The third angle of the triangle containing the 100 angle and the 40 angle is 180-100-40=40. It follows that A is the third angle of the triangle consisting of the found 40 angle and the given 110 angle. Thus, A is a 180-110-40=30 angle, and so the answer is B.

Answer: D
Solution:
Let f represent one fish, l a loaf of bread, and r a bag of rice. Then: 3f=2l, l=4r.
Substituting l from the second equation back into the first gives us 3f=8r. So each fish is worth 8/3 bags of rice.

Answer: C
Solution:
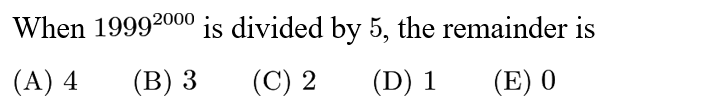
Answer: D
Solution:
Note that the units digits of the powers of 9 have a pattern: 9,1, 9, 1,… and so on. Since all natural numbers with the same last digit have the same remainder when divided by 5, the entire number doesn't matter, just the last digit. For even powers of 9, the number ends in a 1. Since the exponent is even, the final digit is 1. Note that all natural numbers that end in 1 have a remainder of 1 when divided by 5. So, our answer is 1.
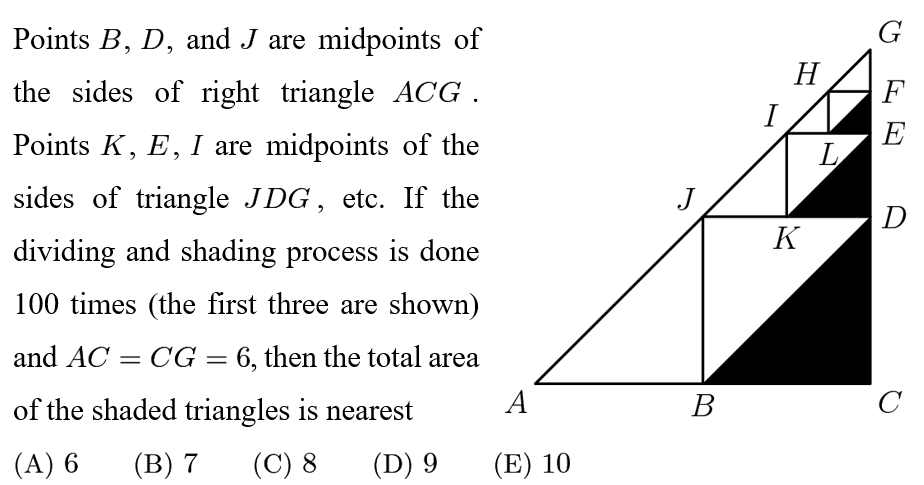
Answer: A
Solution:
All triangles are right-isosceles triangles.
Area(CBD) =1/2*3*3=9/2;
Area(DKE)=1/2*3/2*3/2=9/8;
Area(FLE)=1/2*3/4*3/4=9/32;
The sum of the areas forms a geometric series: 9/2+9/8+9/32+9/128+… This is the sum of a geometric series with first term a1=9/2 and common ratio r=1/4 This is the easiest way to do this problem.
The sum of an infinite geometric series with |r|<1 is shown by the formula s=a1/(1-r)=(9/2)/(1-1/4)=6 giving an answer of A.
中文解析:
图中涉及的大三角形,及黑色的各个小三角形都是直角三角形。
三角形BCD的面积是大三角形ACG的1/4.
三角形KDE的面积是三角形JDG的1/4, 而三角形JDG的面积也是大三角形ACG的1/4. 因此三角形KED的面积是大三角形ACG的 1/4*1/4.
三角形LEF的面积是三角形IEG的1/4. 而三角形IEG的面积是三角形JDG的1/4. 因此,扫侥幸LEF的面积是大三角形ACG的1/4*1/4*1/4.
这些越来越小的三角形的面积的规律是: 1/4, (1/4)*(1/4),(1/4)*(1/4)*(1/4),...... 是等比数列,其中r=1/4. 第一项是1/4. 按照等比数列求和公式, a1/(1+r) = (1/4)/(1-1/4)=1/3. 大三角形的面积是: 1/2 * 6*6=18. 因此题目求得黑色三角形的面积和是1/3 * 18=6. 答案是A。
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,